It is known that chemical reactions in solution are related to the activity of reactants and products. The activity of an ion refers to its effective concentration in chemical reactions. Due to electrostatic interactions between ions in solution, their free movement and reactivity are thus affected, causing discrepancies between their effective and actual concentrations. If ci denotes the equilibrium concentration of ion i (usually represented as [i]) and ai denotes the activity, then their relationship can be expressed as:
| (1) |
The proportionality constant γi is called the activity coefficient of ion i, which reflects the deviation between a real solution and an ideal solution. For strong electrolyte solutions, when the solution concentration is extremely dilute, the distance between ions becomes quite large, making their mutual force negligible. At this point, they can be considered as an ideal solution, and the ion’s activity coefficient can be regarded as 1, i.e., ai = ci.
Currently, there is no good quantitative method for calculating the activity coefficient of ions in high-concentration electrolyte solutions due to the complexity of the situation. However, for dilute solutions (≤ 0.1mol ⋅ L−1), the Debye-Hückel equation can be used:
| (2) |
where zi is the charge of ion i, B is a constant (equal to 0.00328 at 25∘C), ai is the ion volume parameter, approximately equal to the effective radius of the hydrated ion in pm (10−12 m), and I is the ionic strength of the solution. When the ionic strength is small, the size of the hydrated ion can be ignored, and the activity coefficient can be calculated using the Debye-Hückel limiting law:
| (3) |
This formula can also be used for approximate calculations.
The ionic strength I is related to the concentration of various ions in the solution and their charges. The ionic strength of a dilute solution can be calculated as follows:
| (4) |
According to Bronsted’s proton theory, any substance that can donate protons is an acid, and any substance that can accept protons is a base. Substances that can both donate and accept protons are amphiprotic species.(For instance, H2O is an amphiprotic specie because it can donate a proton to form OH- and accept a proton to form H3O+.) Acid-base reactions are the process of proton exchange between acids and bases.
| Acid | Base | Conjugate Base/Acid |
| HCl | H2O | Cl− |
| H 2 SO 4 | H 2 O | HSO 4 − |
| H3PO4 | H2O | H2PO4− |
| H2CO3 | H2O | HCO3− |
| H2O | NH3 | OH− |
| H2O | HS− | OH− |
The following types of reactions are considered acid-base reactions in solution:
Proton Transfer Between Solvent Molecules: Also known as autoprotolysis, such as:
| (5) |
| (6) |
Dissociation of Acid-Base Solutes: The dissociation of acids or bases in solvent molecules, e.g.,
| (7) |
Neutralization Reactions: Usually the reverse of dissociation reactions, commonly used in acid-base titration:
| (8) |
| (9) |
Hydrolysis Reactions: Typical of weak acids and bases, where a weak acid or base dissociates slightly in water, such as:
| (10) |
| (11) |
In the previous discussion, the expression of the equilibrium constant of the reaction was represented by the equilibrium concentrations of the relevant components. In fact, it can also be expressed using activities or a combination of concentrations and activities. Suppose the chemical reaction in the solution is:
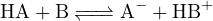
When both reactants and products are expressed in terms of activities, the equilibrium constant is:
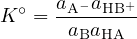
This 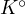 is called the thermodynamic constant, and its value depends on the temperature.
is called the thermodynamic constant, and its value depends on the temperature.
If all components are expressed in terms of equilibrium concentrations, then:
![− +
K = [A--][HB--]
[B][HA ]](calculation14x.png)
This equilibrium constant 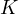 is called the concentration constant. The relationship between
is called the concentration constant. The relationship between 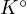 and
and 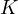 is:
is:
![a − a + [B][HA ] γ − γ +
K ∘ =--A−--HB+- ⋅-------= K ⋅-A---HB-
[A ][HB ] aBaHA γBγHA](calculation18x.png)
It can be seen that the concentration constant is not only related to temperature but also to the ionic strength of the solution. The concentration constant is only constant when both temperature and ionic strength are fixed.
If 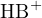 is expressed in terms of activity and other components in terms of concentration, the equilibrium
constant expression for the above reaction is:
is expressed in terms of activity and other components in terms of concentration, the equilibrium
constant expression for the above reaction is:
![[A− ]aHB+
Kmix =-[B][HA-]-](calculation20x.png)
This 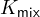 is called the mixed constant. Obviously,
is called the mixed constant. Obviously, 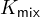 is also related to temperature and
ionic strength. In practical work, since the activities of
is also related to temperature and
ionic strength. In practical work, since the activities of 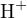 or
or 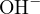 can be easily measured using a
pH meter, they are often expressed in terms of activities, while other relevant components are mostly
expressed in terms of concentrations. In this case, it is more convenient to use the mixed constant for
calculations.
can be easily measured using a
pH meter, they are often expressed in terms of activities, while other relevant components are mostly
expressed in terms of concentrations. In this case, it is more convenient to use the mixed constant for
calculations.
In the treatment of acid-base equilibrium in analytical chemistry, since the solution concentration is generally small, the effect of ionic strength is usually ignored, and the activity constant is used instead of the concentration constant for related calculations. This approach can meet the requirements of general work, but when more precise calculations are needed, such as calculating the pH of standard buffer solutions, the effect of ionic strength on chemical equilibrium should be considered.
The expression of the acid-base equilibrium constant is the basic relationship for acid-base equilibrium calculations. However, relying solely on this relationship to handle acid-base equilibrium problems can often encounter difficulties. It becomes much easier if other equilibrium relationships present in the solution are considered. The following are some commonly used equilibria.
Material balance refers to the total concentration (i.e., analytical concentration  ) of a given substance in a
chemical equilibrium system being equal to the sum of the equilibrium concentrations of all relevant species. The
mathematical expression is called the material balance equation (MBE). For example, the material balance for a
solution with concentration
) of a given substance in a
chemical equilibrium system being equal to the sum of the equilibrium concentrations of all relevant species. The
mathematical expression is called the material balance equation (MBE). For example, the material balance for a
solution with concentration  of
of 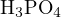 is:
is:
![[H3PO4 ]+ [H2PO4 − ]+ [HPO42 − ]+ [PO43− ] = c](calculation28x.png)
Similarly, for a solution with concentration  of
of 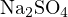 , the material balance equations related to
, the material balance equations related to 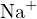 and
and 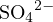 can be written as:
can be written as:
![+ 2− −
[Na ] = 2c, [SO4 ]+ [HSO4 ]+ [H2SO4] = c](calculation33x.png)
Since the solution is electrically neutral, the amount of positive charge carried by cations in the same solution
should equal the amount of negative charge carried by anions. This is known as charge balance. The
expression considering the charge numbers and concentrations of various ions is called the charge balance
equation (CBE). For example, in a solution with concentration  of
of 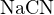 , the following reactions
occur:
, the following reactions
occur:
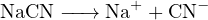
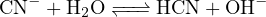
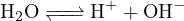
Thus, the amount of positive charge carried by cations in the solution is ![+ +
[H ]+ [Na ]](calculation39x.png) , and the amount of
negative charge carried by anions is
, and the amount of
negative charge carried by anions is ![− −
[CN ]+ [OH ]](calculation40x.png) . Since the solution is electrically neutral, they are
equal:
. Since the solution is electrically neutral, they are
equal:
![+ − −
[H ]+ c = [CN ]+ [OH ]](calculation41x.png)
For a solution with concentration  of
of 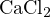 , based on the following reactions:
, based on the following reactions:
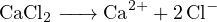
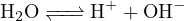
The cations in the solution are 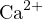 and
and 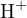 , and the anions are
, and the anions are 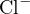 and
and 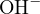 . Since
. Since 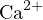 carries
two positive charges, the charge balance equation should multiply
carries
two positive charges, the charge balance equation should multiply ![2+
[Ca ]](calculation51x.png) by 2 to ensure that the units of charge
amounts represented by the ion concentrations are the same. Therefore, the charge balance equation
is:
by 2 to ensure that the units of charge
amounts represented by the ion concentrations are the same. Therefore, the charge balance equation
is:
![+ 2+ − −
[H ]+ 2[Ca ] = [OH ]+ [Cl ]](calculation52x.png)
According to the proton theory of acids and bases, the essence of acid-base reactions is the transfer of protons. The result of acid-base reactions in the solution is that some substances lose protons, and some substances gain protons. Clearly, the amount of protons gained by substances (i.e., bases) should equal the amount of protons lost by substances (i.e., acids). This is known as proton balance. The expression considering the number of protons gained or lost and the concentrations of relevant components is called the proton balance equation (PBE).
Since there are often multiple acid-base components in the solution, it is necessary to know which components gain protons and which lose protons when writing the proton balance equation. When determining who gains or loses protons, some acid-base components are usually chosen as reference levels (reference level or zero level). Compared to these reference levels, components with fewer protons are the proton-losing products, and those with more protons are the proton-gaining products. The reference level is usually chosen as the original acid-base components or the acid-base components that are present in large amounts and directly related to proton transfer in the solution. It is worth noting that for the same substance, only one species can be chosen as the reference level. Additionally, when dealing with polyprotic acids and bases, some components may transfer more than one proton, and a corresponding coefficient should be multiplied in front of the equilibrium concentration representing the amount of protons.
For example, consider an aqueous solution of 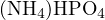 . Using
. Using  ,
, 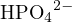 , and
, and 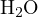 as reference
levels, the proton-gaining products are
as reference
levels, the proton-gaining products are 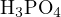 ,
, 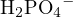 , and
, and 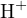 , and the proton-losing products are
, and the proton-losing products are  ,
,
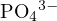 , and
, and 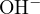 . The proton balance equation is:
. The proton balance equation is:
![[H+ ]+ [H2PO4 − ]+ 2[H3PO4 ] = [OH− ]+ [PO43− ]+ [NH3 ]](calculation63x.png)
Sometimes, when acid-base components dissolve in water, significant acid-base reactions occur, and the main
acid-base components present in the solution are no longer the original acid-base components. In this case, the
original acid-base components can still be used as reference levels, and the amount of protons gained or lost remains
equal. For example, in a solution with concentration  of
of 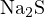 , the original acid-base components
, the original acid-base components
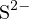 and
and 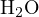 can be chosen as the proton reference levels. Thus, the proton-gaining products are
can be chosen as the proton reference levels. Thus, the proton-gaining products are
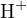 ,
, 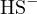 , and
, and 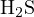 , and the proton-losing product is
, and the proton-losing product is 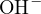 . The proton balance equation
is:
. The proton balance equation
is:
![+ − −
[H ]+ [HS ]+ 2[H2S] = [OH ]](calculation72x.png)
For acid-base conjugate systems, they can be regarded as mixtures of weak acids with strong bases or strong acids
with weak bases. Therefore, the proton reference levels can be chosen as the corresponding weak acids with strong
bases or strong acids with weak bases. For example, in a solution of 0.2 mol/L 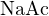 and 0.1 mol/L
and 0.1 mol/L
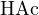 , the proton reference levels can be chosen as
, the proton reference levels can be chosen as 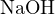 (0.2 mol/L, i.e., strong base),
(0.2 mol/L, i.e., strong base), 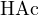 , and
, and
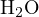 , or
, or 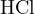 (0.1 mol/L, i.e., strong acid),
(0.1 mol/L, i.e., strong acid), 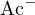 , and
, and 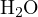 . The proton balance equation
is:
. The proton balance equation
is:
![[Na+ ]+[H+ ] = [Ac − ]+ [OH − ]](calculation81x.png)
The Henderson-Hasselbalch equation is a widely used formula in buffer solution equilibrium calculations. It is derived from the material balance equation (MBE) and charge balance equation (CBE) for a weak acid solution. The derivation process is as follows:
Consider a buffer solution containing a weak acid 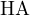 and its conjugate base
and its conjugate base 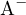 . The dissociation reaction of
. The dissociation reaction of
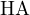 is:
is:
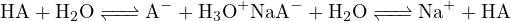
Let [HA] = ca and [A−] = cb. From the Material Balance Equation we have:
![[Na+ ] = ca[HA ]+ [A − ] = ca + cb](calculation86x.png)
From the Charge Balance Equation we have:
![+ + − −
[Na ]+ [H ] = [A ]+ [OH ]](calculation87x.png)
Cross multiplying the above two equations, we get:
![− + − + −
[A ] = cb + [H ]− [OH ][HA] = ca − [H ]+ [OH ]](calculation88x.png)
Substitute the above two equations into the equilibrium constant expression:
![[A− ][H+ ] cb + [H+ ]− [OH− ][H+ ]
K = -[HA-]--= --c-−-[H+-]+-[OH−-]--
a](calculation89x.png)
As [H+] and [OH−] are negligible compared to ca and cb, the equation can be simplified to:
![cb[H+]
K = -c----
a](calculation90x.png)
And therefore, the Henderson-Hasselbalch equation is derived:
![[A-− ]
pH = pK + log [HA ]](calculation91x.png)
And that also explains why the Henderson-Hasselbalch equation is only applicable to weak acid solutions. Since the dissociation of weak acids is incomplete, the concentrations of HA and A− are not significantly affected by the presence of H+ and OH−.
Now that we have discussed the basic principles of acid-base equilibrium calculations, and the material balance, charge balance, and proton balance equations. From any two of the MBE, CBE, and PBE, the equilibrium concentrations of all relevant components in the solution can be calculated.
class Acid: def __init__(self, Ka=None, pKa=None, charge=None, conc=None): self.pKa = np.array([pKa] if pKa else -np.log10(Ka), dtype=float) self.pKa.sort() self.Ka = 10**(-self.pKa) self.charge = np.arange(charge, charge - len(self.Ka) - 1, -1) self.conc = conc def alpha(self, pH): h3o = 10.**(-np.array([pH] if isinstance(pH, (int, float)) else pH, dtype=float)) h3o_pow = h3o**np.arange(len(self.Ka) + 1)[::-1] Ka_prod = np.cumprod(np.append(1., self.Ka)) h3o_Ka = h3o_pow * Ka_prod den = h3o_Ka.sum(axis=1) if len(h3o.shape) > 1 else h3o_Ka.sum() return h3o_Ka / den.reshape(-1, 1) if len(h3o.shape) > 1 else h3o_Ka / den
The above code defines a class Acid that can be used to calculate the dissociation of acids. The alpha method calculates the degree of dissociation of the acid at a given pH value.
It is related to the MBE as the sum of the equilibrium concentrations of all relevant species should equal to 1. This is a very import constraint in the calculation of the equilibrium concentrations of all relevant species.
def ChargeBalance(acid, pH): Kw = 1.1e-14 h3o = 10**(-pH) oh = Kw / h3o alpha = acid.alpha(pH) pos = h3o + sum(alpha[acid.charge > 0] * acid.conc * acid.charge[acid.charge > 0]) neg = oh + sum(alpha[acid.charge < 0] * acid.conc * abs(acid.charge[acid.charge < 0])) return pos, neg
The above code defines a basic function ChargeBalance that calculates the positive and negative charges in the solution at a given pH value. With this code, we can plot the charge balance curve of a solution. Here we use (NH4)3(PO4) as an example.
The positive charges can be calculated as:
![P = [H+ ]+ 3[NH4+ ]](calculation92x.png)
The negative charges can be calculated as:
![− 3− 2− −
N = [OH ]+ 3× [PO4 ]+ 2 × [HPO4 ]+ [H2PO4 ]](calculation93x.png)
3po4-CBE.png)
3po4-CBE_tot_err.png)
From the above figures (1 and 5), we can see that the positive and negative charges are equal at the isoelectric point, which is the point where the solution is electrically neutral.
3po4-CBE-tot-abs.png)
Therefore we can use a minimization algorithm to find the isoelectric point of the solution. For example, we can use the scipy.optimize.minimize function to find the pH value where the absolute charge balance error is minimized. I have used the Nelder-Mead method to find the isoelectric point of (NH4)3(PO4).
| (12) |
Below is the code implementation of the CBE_calc class that calculates the isoelectric point of a solution.
class CBE_calc: def __init__(self, *species, Kw=1.01e-14): ... def Charge_diff(self, pH): ... def pH_calc(self, start=7.0, method='Nelder-Mead', tol=1e-5): result = minimize(self.Charge_diff, start, method=method, tol=tol) self.pH = result.x[0] if result.x.size == 1 else result.x
The same calculation method of the charge balance equation can be used to calculate the proton balance equation. However, the Proton Balance Equation is more complex than the Charge Balance Equation, as it involves the dissociation of acids and bases. Proton Balance Equation requires a reference level to determine which components gain or lose protons.
For instance, still using (NH4)3(PO4) as an example, the proton balance equation can be written as:
![+ −
Gain = [H ]+ [H2PO4 ]+ 2× [H3PO4]](calculation95x.png)
![Loss = [NH3]+ [OH − ]+ 3× [PO43− ]](calculation96x.png)
3po4-PBE.png)
3po4-PBE-tot-err.png)
Figure 5 shows the gain and loss proton curves of (NH4)3(PO4), and Figure 5 shows the proton balance error curve of (NH4)3(PO4). The isoprotonic point is the point where the gain and loss protons are equal. We can see that PBE calculation gives the same result as CBE calculation.
In this paper, we have explored the fundamental principles of acid-base equilibrium calculations, focusing on the Material Balance Equation (MBE), Charge Balance Equation (CBE), and Proton Balance Equation (PBE). These equations are essential tools for understanding and predicting the behavior of acid-base systems in solution.
We demonstrated the derivation and application of these equations through various examples, including the calculation of equilibrium constants and the use of the Henderson-Hasselbalch equation for buffer solutions. Additionally, we implemented Python code to calculate the dissociation of acids and the charge balance in solutions, providing a practical approach to solving complex equilibrium problems.
The graphical analysis of (NH4)3(PO4) using CBE and PBE highlighted the importance of these equations in identifying the isoelectric point, where the solution is electrically neutral. Both CBE and PBE calculations yielded consistent results, underscoring their reliability in acid-base equilibrium studies.
Overall, the integration of theoretical principles with computational tools offers a comprehensive framework for analyzing acid-base equilibria, facilitating more accurate and efficient solutions to chemical equilibrium problems.
The codes and data used in this paper are available on GitHub at Github.com/Eric-xin/pH_Calculation. The code is written in Python and can be run in any Python environment with the required libraries installed. Jupyter notebooks are also provided for interactive exploration of the calculations and results.
[1] P. W. Atkins, J. De Paula, and J. Keeler, Atkins’ physical chemistry. Oxford university press, 2023.
[2] G. D. Christian, P. K. Dasgupta, and K. A. Schug, Analytical chemistry. John Wiley & Sons, 2013.
[3] C. Macca, “The formulation of the electron and proton balance equations for solving complicated equilibrium problems in redox titrations,” Fresenius’ journal of analytical chemistry, vol. 357, pp. 229–232, 1997.
[4] E. I. Volcke, S. Van Hulle, T. Deksissa, U. Zaher, and P. Vanrolleghem, “Calculation of ph and concentration of equilibrium components during dynamic simulation by means of a charge balance,” Ghent: Ghent University, 2005.
[5] “GitHub - rnelsonchem/pHcalc: Systematic pH calculation package for Python — github.com,” https://github.com/rnelsonchem/pHcalc, [Accessed 02-11-2024].